Вопросы классификации систем планирования машиностроительного производства
На базе систем ERP, APS, MES и SCADA возможно построение глубоко структурированных систем управления предприятием, начиная от функций стратегического планирования до управления технологическими процессами [1]. Системы класса PDM/PLM являются необходимым дополнением с точки зрения формирования на предприятии хранилища данных об изделиях в сочетании с функцией интеграции конструкторской и технологической информации [2].
При создании, а также выборе систем планирования очень важно знать функциональные возможности как моделей и алгоритмов, так и самой системы планирования. Для того чтобы идентифицировать эти возможности, необходимо, прежде всего, обратиться к классификации систем планирования.
Несмотря на то, что основы классификации моделей планирования лежат в классификации задач расписаний [3, 4], модели систем планирования производства для предприятий машиностроения имеют большое количество технологических и организационных параметров, присущих производственным системам дискретного характера, которые в классическом варианте теории расписаний не учитываются. Кроме того, серьезную путаницу вносят классификационные признаки систем планирования, которые появились благодаря развитию операционного менеджмента, различных общественных инженерных обществ, фирм-производителей программного обеспечения, когда в целях маркетинговой политики создаются собственные признаки, зачастую малоинформативные, как отражение торговой марки программного продукта. Например, в настоящее время достаточно популярным признаком классификации систем планирования являются понятия pull planning (вытягивающее планирование) и push planning (выталкивающее планирование). Большинство специалистов сходятся во мнении, что отличие систем первого типа от последних заключается в более гибком воздействии на общее расписание, когда приоритет на выполнение операций в цеху отдается тем или иным деталям. Но если обе системы работают по некоему алгоритму, ничто не мешает в любой момент пересчета расписания установить приоритетный выпуск той или иной продукции в обоих типах систем. Внесение в функциональность систем планирования критериев из теории массового обслуживания, таких как FIFO, SIO, LRT и др. [5], относится не к классификации систем, а к обоснованию эвристического правила выбора текущей работы из всего пула работ.
Чтобы идентифицировать ту или иную систему планирования и соотнести ее с конкретными требованиями производства, необходима более полная классификация, отражающая особенности технологии и организации.
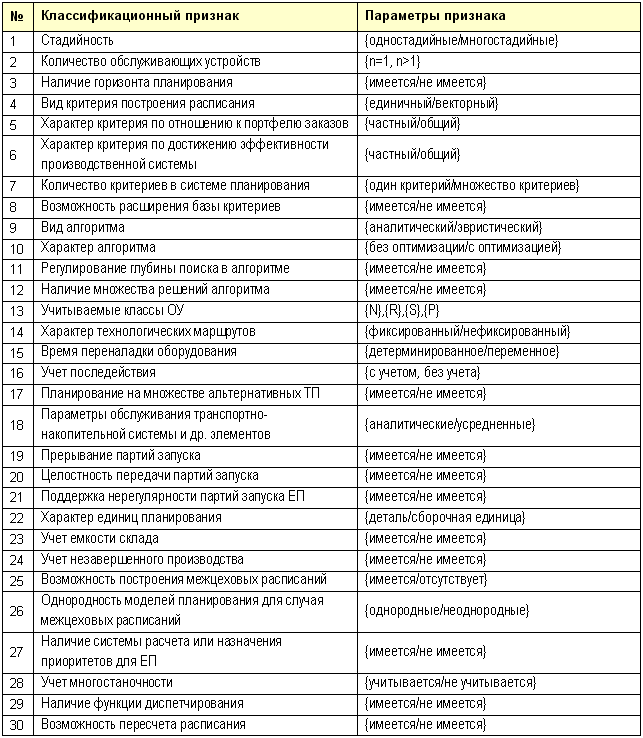
Рассмотрим предлагаемую автором классификацию на примере и подробном анализе таблицы классификационных признаков систем планирования.
Признаки стадийности и количества обслуживающих устройств (ОУ) являются основополагающим признаком в теории расписаний [3, 4]. В задачах составления расписаний в любых системах планирования эти признаки классификации также являются справедливыми. Технологический процесс (ТП) изготовления большинства деталей в механической обработке состоит, как правило, из нескольких стадий – операций. Поэтому однооперационные ТП можно рассматривать как частный случай многооперационных. Вариант с количеством ОУ n>1 встречается чаще всего, а случай с n=1 встречается в тех случаях, когда все оборудование сгруппировано, чаще всего, в производственную линию с технологическим оборудованием, расположенным согласно ТП изготовления некой единицы планирования (ЕП), в качестве которой могут выступать отдельные детали или узлы.
Наличие горизонта планирования для всего множества заказов, присутствующих во множестве
говорит о том, что алгоритм системы планирования будет пытаться построить расписание в пределах этого горизонта. Отсутствие такого горизонта чаще всего характерно для систем планирования, в которых используется однопроходный эвристический алгоритм и в случае превышения горизонта планирования расписание не будет улучшаться. При выборе конкретных систем рекомендуется вариант с наличием горизонта планирования.
Признак «Вид критерия построения расписания» определяет – используется один некий критерий
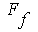или несколько, которые представлены вектором или функционалом
,
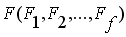состоящим из нескольких отдельных критериев. Во втором случае использование векторного критерия позволяет заложить в расписание сразу несколько требовании – минимизация состава и длительности операций по переналадке оборудования, равномерность загрузки оборудования и др.
Классификационные признаки систем планирования
Использование такого функционала накладывает дополнительные требования на алгоритм построения расписания, поскольку как допустимое, так и оптимальное решение, чаще всего, ищется в области компромиссов, – на области Парето [6].
Кроме того, количество отдельных критериев в таком функционале не может быть велико, так как их количество сказывается на эффективности получаемого решения, не говоря уже о том, что отдельные критерии, входящие в функционал, не должны быть противоречивы.
Характер критерия по отношению к портфелю заказов определяет, относится ли тот или иной критерий только к одной ЕП или некой группе из нескольких ЕП, либо этот критерий относится ко всей программе выпуска (портфелю заказов) и всему парку оборудования. Например, критерий минимума состава и длительности переналадок оборудования является общим как для всего парка оборудования, для которого ведется планирование, так и для всего портфеля заказов. Напротив, критерий минимума тех же затрат по переналадке по отношению к какой-либо конкретной i-й ЕП из портфеля заказов – это уже частный критерий. Частный критерий по отношению к портфелю заказов всегда выделяет ту или иную ЕП (или группу ЕП) относительно остальных ЕП во множестве M.
Характер критерия по достижению эффективности производственной системы определяет направленность критерия либо на конкретный показатель, либо на общий. Например, указанный ранее критерий минимума состава и длительности переналадок оборудования является частным, поскольку его выполнение гарантирует только минимизацию данных затрат. Затраты на транспортных и складских операциях, а также пролеживание ЕП при этом могут и возрасти. Надо сказать, что в этом плане большинство единичных критериев планирования относятся к частным по данному квалификационному признаку. Даже незыблемые вроде бы критерии типа минимума продолжительности выполнения всего плана работ также относятся к частным. Например, если во множестве M не две-три операции, а значительно больше, как это и бывает в реальных случаях (в мелкосерийном производстве участок из 100 ОУ за смену может «переварить» до 300 операций), оптимальному решению при использовании данного критерия всегда соответствует хотя бы одна последовательность операций a, b,…, c на некой ЕП, для которой суммарное время выполнения этой последовательности T нельзя уменьшить. Пример такой последовательности показан на рис.1. Хорошо, если мы сразу, на первых же итерациях поиска получили плотный по загрузке оборудования вариант «а», который высвободит нам сразу несколько ОУ. При этом высвободившихся рабочих мы можем переместить на другие участки, где есть потребность в рабочей силе. Если же получим вариант «б», характеризующийся, как мы видим, весьма неэффективным распределением операций между ОУ, то дальнейший поиск нам ничего не даст, т.к. величину длительности выполнения всего множества работ – T, мы не уменьшим. Алгоритм, руководствуясь таким критерием, честно просмотрев все варианты, даст нам график загрузки в виде «лоскутного одеяла», характеризующийся простоями оборудования, которые должны быть оплачены. Частный критерий в данном случае – это критерий, который отражает какую-либо одну особенность при построении расписания.
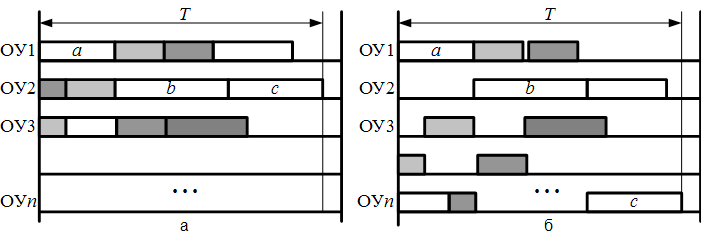
Рис.1. Особенности использования критерия минимизации
Количество критериев в системе планирования обычно бывает больше одного. Диспетчеру предлагается, исходя из конкретной производственной ситуации, выбрать тот или иной критерий планирования на расчетный период времени. Чем больше критериев в системе планирования, тем больше гибкость планирования и выше качество принимаемых решений. Системы с одним критерием встречаются достаточно редко и чаще всего относятся к классу APS. При этом единственный критерий планирования может отражать прибыль предприятия, полученную за единицу времени. В системах класса MES количество критериев планирования всегда должно быть больше одного.
Возможность расширения базы критериев как функция настройки системы пользователем, которому предоставляется возможность формирования определенных выражений с помощью базового алфавита и логических правил, встречается достаточно редко. Несмотря на то, что эта возможность резко повышает гибкость системы в плане настройки под конечного пользователя, имеются определенные сложности в реализации алгоритма построения расписания.
Вид алгоритма в системе планирования может быть декларирован какой угодно, но будет лучше, если эти декларации не будут носить маркетинговый характер, поскольку для нелинейных задач планирования, к которым относится подавляющее большинство аналогичных производственных задач, невозможно построить аналитический алгоритм, не свободный от известных проблем вычислительной сложности (NP-сложность). Практически все известные автору алгоритмы планирования для производственных систем всегда используют эвристический алгоритм. Тем не менее, ряд эвристических алгоритмов имеют очень неплохие показатели.
Характер алгоритма с точки зрения оптимизации говорит о том, что либо в системе при построении расписания используется процесс оптимизации, либо не используется. В первом случае не только появляется возможность нахождения улучшенного варианта расписания, то и повышается вероятность нахождения допустимого варианта за счет самой процедуры оптимизации. Второй случай является малопредпочтителеным. Проверить наличие функции оптимизации в алгоритме той или иной системы со стороны пользователя крайне сложно, поскольку алгоритм и программный код обычно защищены со стороны разработчика системы, хотя в практике имеются случаи, когда это можно было определить по косвенным показателям. Например, в работе [7] Д. Трич описывает ситуацию, когда покупатель предъявил и выиграл судебный иск против компании Э. Голдратта именно по вопросу об отсутствии заявленной оптимальности в системе планирования. Алгоритмы, получающие полностью оптимальное решение – крайне редкое явление, поскольку они в большинстве случаев используют, как уже было сказано выше, эвристические методы, которые, как правило, либо не обладают сходимостью, либо время сходимости столь велико, что о полной оптимизации можно забыть.
Регулирование глубины поиска в алгоритме – желательно, поскольку это позволяет в ряде случаев, не столь сильно ограниченных лимитом времени вычислений, получать лучшие решения относительно достигнутого допустимого.
Наличие множества решений алгоритма характерно для алгоритмов, имеющих процедуры оптимизации. Эта возможность, хотя и не так часто встречается ввиду сложности построения алгоритма, весьма полезна, поскольку позволяет получать диспетчеру ряд допустимых решений, из которых он может выбрать наиболее привлекательное по тем или иным конкретным причинам, не учтенным в аналитической форме.
Учитываемые классы ОУ – это признак, который говорит о том, какие классы ОУ могут быть учтены при построении расписания работы производственной системы. Традиционно в системах планирования учитывается только один класс ОУ – рабочие центры (РЦ) в виде множества технологического оборудования
.
Расписания для других классов ОУ – множества
транспортных средств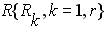
,
складских систем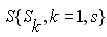
,
бригад наладчиков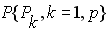
если и строятся, то, как правило, методом проекций [8] в виде расписаний, производных от расписаний основных ОУ – множества N. Это приводит не только к тому, что в дальнейшем они могут быть невыполнимы, но и к тому, что количество ОУ классов R, S, P получается сильно завышенным при крайне низкой загрузке. Например, при использовании существующих методов построения расписаний для вспомогательных ОУ их характер загрузки часто подчиняется Парето-распределению – степенная функция вида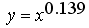
, а при использование комплексной модели, которая учитывает в расписании все классы ОУ, – равномерному распределению (рис.2,а). Парето-распределение, которое получается в традиционных расписаниях, – весьма неблагоприятный вид распределения, который говорит о том, что 80% всей полезной работы приходится на 20% ОУ.
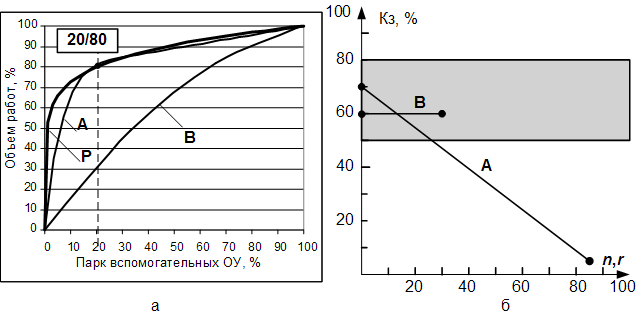
Рис.2. Последствия учета различных классов ОУ при различных подходах:
А – существующие подходы к учету ОУ; P – Парето-распределение; B – комплексные методы учета ОУ в расписаниях
До сих пор считалось, что Парето-распределение характеризует только социально-экономические процессы в обществе. Исследования, проведенные автором, показали, что принцип самоорганизации для технических систем, а метод проекций – это, по сути, и есть метод самоорганизации, является проигрышным вариантом. Использование комплексного подхода учета вспомогательных ОУ в моделях расписаний [8] показало, что: 1) сокращение количества вспомогательных ОУ достигает с 2-х до 10 раз; 2) повышение коэффициента загрузки вспомогательных ОУ достигает до 80%; 3) появляется возможность построения расписаний и возможность формирования управляющих программ для ОУ. Исходя из этого, крайне желательно, чтобы система планирования учитывала все интересующие производственников классы ОУ.
Характер технологических маршрутов по определению в теории расписаний может быть как фиксированным, так и не фиксированным. В первом случае ЕП проходят согласно ТП строго через определенные единицы технологического оборудования. Во втором случае появляется возможность пропустить те или иные ЕП через РЦ, которые являются альтернативными по методам обработки и достижимым параметрам точности и качества обработки. С точки зрения оптимальности получаемого расписания более предпочтительным является случай с нефиксированными маршрутами. При этом перед началом процесса планирования необходимо сформировать группы альтернативных РЦ.
Время переналадки оборудования в соответствии с характером технологических маршрутов может быть детерминированным или недетерминированным. В первом случае длительности всех операций ЕП считаются постоянными для любого РЦ из альтернативной группы оборудования (количество РЦ в альтернативной группе больше единицы). Во втором случае время переналадки зависит от того, на каком РЦ из альтернативной группы будет выполняться та или иная ЕП. Второй случай более предпочтительней, поскольку позволяет сэкономить, в среднем, 2-3% времени по отношению к усредненному варианту назначения указанных времен.
Учет последействия касается вопроса особенностей учета переналадки оборудования. Традиционный подход к определению величины состава и длительности операции переналадки РЦ заключается в том, что учитываются все требуемые операции из всего требуемого комплекса переналадок РЦ. При этом считается, что оборудование РЦ (станок, промышленный робот, накопитель деталей и пр.) в технологическом плане не соответствует вновь поступающей партии ЕП. Естественно, что в этом случае длительность комплекса переналадок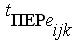
принимается как максимальная с точки зрения длительности. При учете последействия вводится понятие состояния РЦ с точки зрения имеющихся на момент поступления на РЦ новой 
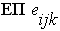технологических ресурсов [8].
Например, состав и длительность комплекса переналадок какой-либо k-й единицы РЦ с соответствующим составом ресурсов при поступлении партии ЕП зависит не только от требуемого состава технологических ресурсов для выполнения этой ЕП – , но также от состояния РЦ , которое сложилось на рассматриваемый момент назначения на всей предыстории планирования РЦ в течение смены (рис.3). При этом состав и длительность комплекса переналадок РЦ может изменяться от нуля (рис.3.а), – случай, когда все требуемые ресурсы , необходимые для выполнения ЕП имеются в составе РЦ, до максимального значения (рис.3.в), – в этом случае множество не включает в себя множество . Данный метод учета переналадок позволяет существенно повысить точность составления расписания и загрузку РЦ.
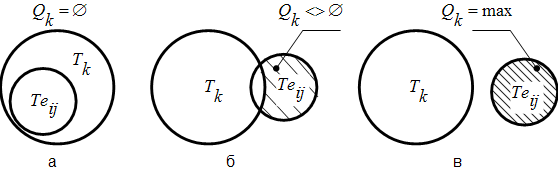
Рис.3. Учет последействия при оценке переналадок
Планирование на множестве альтернативных ТП, которое существенно повышает гибкость планирования и загрузку оборудования, возможно только в том случае, если имеющаяся САПР ТП поддерживает возможность формирования множества альтернативных ТП (АТП) по отношению к базовому варианту. Разработка АТП в традиционном варианте – процесс весьма трудоемкий, но если САПР ТП имеет возможность представления ЕП не только в виде операций, но также в виде технологических переходов, то на основе базового варианта ТП при использовании инструмента размерного анализа [9] появляется возможность создания множества АТП по точности не уступающих базовому варианту ТП [10].
Параметры обслуживания транспортно-накопительной системы и др. элементов могут быть как усредненными, так и расчетными (аналитическими). Первый случай, который является общепринятым, является допустимым, но во втором случае, когда, например, время транспортирования для транспортного средства определяется с учетом вычисленного кратчайшего маршрута, или аналитически определяются длительности всех вспомогательных операций [8], повышается точность составления расписания.
Прерывание партий запуска является классической характеристикой расписаний [3, 4]. Возможность прерывания появляется только для непрерывных процессов без последействия, например, для вычислительных систем. В машиностроении, которое характеризуется дискретным характером производства, прерывания партий запусков нежелательны как с точки зрения невозможности прерывания большинства операций по технологическим причинам, так и по причине возрастания количества и общей длительности процессов переналадки оборудования.
Целостность передачи партий запуска отражает возможность передачи уже обработанных отдельных ЕП (деталей, узлов) на другую операцию, не дожидаясь окончания выполнения всей партии ЕП. Если такая возможность имеется (отсутствует требование по целостности партии запуска при передаче), то это значительно повышает гибкость планирования и плотность загрузки оборудования (рис.4), однако реализация этой возможности имеет определенные сложности в плане построения алгоритма планирования, поэтому не все системы планирования имеют такую возможность.
Поддержка нерегулярности партий запуска ЕП означает возможность формирования на одном РЦ некой партии из разнородных партий ЕП с общностью по получаемым на технологической операции поверхностям обработки, например, обработка одинаковых по размерам и качеству поверхностей на различных деталях. Такие партии запуска непостоянны и могут образовываться каждый раз для различных деталей на различных операциях, т.е. в данном случае мы имеем дело с запуском в производство укрупненных партий в виде нерегулярных единиц планирования (НЕП), поскольку данные партии, представляющие нерегулярные множества [11]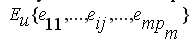
при поступлении на какой-либо k-й РЦ могут образовываться различными как по наименованию ЕП , входящих в НЕП, так и по номеру операции (рис.5). При этом на каком-либо k-м оборудовании будут обработаны детали различных наименований, и данная операция для каждого наименования может быть любой по порядку следования в ТП данной детали [8]. После обработки НЕП каждая ЕП может продолжать свой процесс движения по цеху согласно своему ТП, либо вновь объединяться в НЕП.
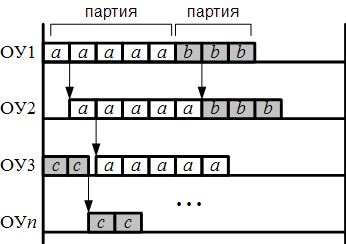
Рис.4. Целостность передачи партии запуска
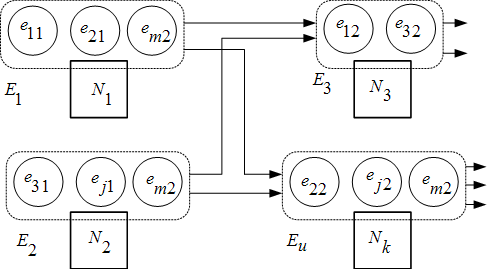
Рис.5. Нерегулярные партии запуска
Нерегулярные партии запуска часто формируются на операциях, которые принято называть технологическими сборами, когда на одной операции, с целью повышения точности сопряжения, обрабатываются две или более деталей, входящих в сборочную единицу. Возможность оперирования нерегулярными партиями запуска в системе планирования – желательна.
Характер единиц планирования указывает на то, чем может оперировать та или иная система планирования – только отдельными деталями или сборочными единицами (комплектами, узлами, готовыми изделиями). Крайне желательным является вариант учета сборочных единиц, поскольку он является наиболее общим случаем. При этом директивные сроки выполнения заказов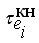
указываются не на отдельные детали, а на сборочную единицу верхнего уровня. Моменты окончания обработки и сборки отдельных деталей и узлов должны определяться в процессе построения расписания исходя из ненарушения сроков .
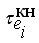Учет емкости склада в системах планирования подразумевает, что планирование всей программы ведется с учетом предельной емкости склада готовой продукции или промежуточного склада. При этом расписание строится исходя из того ограничения, что емкость склада не может быть превышена. Используется в случае, когда склад является лимитирующим фактором. При этом склад в математических моделях является ОУ с соответствующими параметрами: длительностью обслуживания, количеством операторов и пр.
Учет незавершенного производства в подавляющем большинстве случаев должен присутствовать в системе планирования, поскольку этот фактор определяет не только величину связанного капитала, но и общую эффективность производственной системы.
Возможность построения межцеховых расписаний в большей степени присуща APS-системам, но может присутствовать и в MES-системах [8]. Существующие методы построения межцеховых расписаний на основе межцеховой кооперации характеризуются существенными потерями времени ввиду укрупненной оценки времени выполнения заказа тем или иным цехом. Предпочтительным в системах планирования является вариант построения межцеховых расписаний, который оперирует комплексной математической моделью, отражающей критерии и ограничения всех цехов. Такая возможность легко реализуется в APS-системах, поскольку в них чаще всего ведется планирование для всего предприятия по одному критерию – максимизации прибыли за единицу времени. Если межцеховое расписание строится только для определенной группы цехов, то в модели планирования необходимо учитывать ограничения и критерии этих цехов, т.е. переходить к комплексному характеру построения модели планирования [12].
Однородность моделей планирования для случая межцеховых расписаний облегчает построение как моделей, так и расписаний в последствии, но эта однородность наблюдается далеко не всегда, поскольку каждый цех может характеризоваться, в силу конкретных производственных ситуаций, собственными критериями и ограничениями в модели. Желательно, если система планирования в состоянии учитывать неоднородность моделей.
Наличие системы расчета или назначения приоритетов для ЕП означает возможность планирования с учетом приоритетов для тех или иных ЕП. Как мы уже сказали выше, приоритеты типа FIFO и др., взятые из теории массового обслуживания, мало что дают в реальности, поскольку каждая ЕП не только может характеризоваться собственными сроками сдачи, но и трудоемкостью. Поэтому расчет приоритетов должен быть чем-то обоснован, базироваться на анализе проблемы. Например, приоритет ЕП, назначенный на основе напряженности заказов [8] позволяет быстрее выпустить те ЕП, которые имеют минимальный резерв времени. В то же время данная характеристика больше относится к алгоритмической части системы, к анализу номенклатуры запуска перед процедурой планирования.
Учет многостаночности характеризует возможность системы планирования загружать на какие-либо ОУ в один и тот же интервал времени различные работы. Эта характеристика отражает не только реальные случаи многостаночного обслуживания в цеху, но и возможность планирования бизнес-процессов (рис.6), когда за одним и тем же исполнителем закрепляется несколько различных работ.
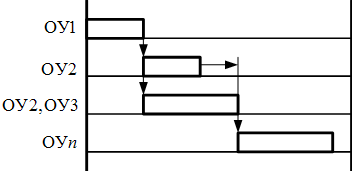
Рис.6. Учет многостаночности
Наличие функции диспетчирования означает возможность контроля хода выполнения исполняемого плана относительно расчетных данных. При этом в режиме времени с дискретой, равной минимальной длительности любого действия (технологическая операция, переналадка оборудования и т.п.), производится анализ запаздывания или опережения всех работ на всех ОУ.
Возможность пересчета расписания появляется только при наличии функции диспетчирования. При этом при пересчете должны учитываться: текущие данные по незавершенному производству, сроки выпуска продукции, возможность использования иных критериев построения расписания работ.
В рассмотренной классификации не приводятся характеристики, которые являются не столь важными с точки зрения качества получаемых решений и более относящихся к технической реализации, например, сетевой или локальный вариант системы планирования, возможность интеграции с системами САПР ТП, PDM/PLM, протоколы передачи данных и пр.
Автор не стал придавать формальный вид характеристикам, как это принято в теории расписаний [3, 4], поскольку при большом количестве характеристик формализация записи теряет смысл краткой нотации. Кроме того, классификация может не исчерпываться указанным составом классификационных признаков, поскольку те или иные особенности конкретного производства могут вносить свои дополнения. Главное при этом, чтобы новые классификационные признаки отражали особенности планирования и качество принимаемого решения.
Таким образом, при выборе системы планирования любого уровня – ERP, APS, MES, необходимо, прежде всего, обратить внимание на важность для конкретного производства тех или иных классификационных признаков и наличие соответствующих функций в выбираемой системе.
При желании на базе рассмотренных классификационных признаков можно решить задачу оптимизации на векторном критерии с целью выбора оптимальной для предприятия системы планирования.
©Загидуллин Р.Р. докт. техн. наук, профессор каф. АТП Уфимского Государственного Авиационного Технического Университета
©12NEWS
Литература
1. Загидуллин Р. Р., Фролов Е. Б. Управление машиностроительным производством с помощью MES-систем. М.: СТИН, 2007, №11, С.2–5.
2. Загидуллин Р. Р., Драган В. Ф., Степанов В. Е., Камалетдинов Т. Р. Интеграция систем конструкторско-технологической подготовки и управления производством в структуре АСУП. М.: СТИН, 2007, №10, С. 2 – 5.
3. Танаев В. С., Гордон В. С., Шафранский Я. М. Теория расписаний. Одностадийные системы. – М.: Наука, – 1984. – 384 с.
4. Танаев В. С., Сотсков Ю. Н, Струсевич В. А. Теория расписаний. Многостадийные системы. – М.: Наука, – 1989. – 328 с.
5. Смоляр Л.И. Модели оперативного планирования в дискретном производстве. – М.: Наука, – 1978, – 320 с.
6. Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. М.: ФИЗМАТЛИТ. – 2002. – 144 с.
7. Д. Трич. Почему метод критического пути под любым другим названием не становится лучше? К созданию целостного подхода к PERT/CRM. Управление проектами и программами. – № 1(05) 2006. – С.4 – 22.
8. Загидуллин Р.Р. Оперативно-календарное планирование в гибких производственных системах. М.: Изд-во МАИ, 2004. – 208 с.
9. Балакшин Б.С. Основы технологии машиностроения. М.: Машиностроение, – 1969. – 358 с.
10. Загидуллин Р.Р. Проектирование и планирование технологических процессов в ГПС на базе дифференциации операций. СТИН, – 2002, – № 6., с. 15 – 19.
11. Рейуорд - Смит В.Дж. Теория формальных языков. Вводный курс: Пер. с англ. – М.: Радио и связь, –1988, – 128 с.
12. Загидуллин Р.Р. Построение моделей межцеховых расписаний в подсистемах оперативно-календарного планирования автоматизированных производств. – СТИН, №8, 2004, С.3 – 8.
При создании, а также выборе систем планирования очень важно знать функциональные возможности как моделей и алгоритмов, так и самой системы планирования. Для того чтобы идентифицировать эти возможности, необходимо, прежде всего, обратиться к классификации систем планирования.
Несмотря на то, что основы классификации моделей планирования лежат в классификации задач расписаний [3, 4], модели систем планирования производства для предприятий машиностроения имеют большое количество технологических и организационных параметров, присущих производственным системам дискретного характера, которые в классическом варианте теории расписаний не учитываются. Кроме того, серьезную путаницу вносят классификационные признаки систем планирования, которые появились благодаря развитию операционного менеджмента, различных общественных инженерных обществ, фирм-производителей программного обеспечения, когда в целях маркетинговой политики создаются собственные признаки, зачастую малоинформативные, как отражение торговой марки программного продукта. Например, в настоящее время достаточно популярным признаком классификации систем планирования являются понятия pull planning (вытягивающее планирование) и push planning (выталкивающее планирование). Большинство специалистов сходятся во мнении, что отличие систем первого типа от последних заключается в более гибком воздействии на общее расписание, когда приоритет на выполнение операций в цеху отдается тем или иным деталям. Но если обе системы работают по некоему алгоритму, ничто не мешает в любой момент пересчета расписания установить приоритетный выпуск той или иной продукции в обоих типах систем. Внесение в функциональность систем планирования критериев из теории массового обслуживания, таких как FIFO, SIO, LRT и др. [5], относится не к классификации систем, а к обоснованию эвристического правила выбора текущей работы из всего пула работ.
Чтобы идентифицировать ту или иную систему планирования и соотнести ее с конкретными требованиями производства, необходима более полная классификация, отражающая особенности технологии и организации.
Рассмотрим предлагаемую автором классификацию на примере и подробном анализе таблицы классификационных признаков систем планирования.
Признаки стадийности и количества обслуживающих устройств (ОУ) являются основополагающим признаком в теории расписаний [3, 4]. В задачах составления расписаний в любых системах планирования эти признаки классификации также являются справедливыми. Технологический процесс (ТП) изготовления большинства деталей в механической обработке состоит, как правило, из нескольких стадий – операций. Поэтому однооперационные ТП можно рассматривать как частный случай многооперационных. Вариант с количеством ОУ n>1 встречается чаще всего, а случай с n=1 встречается в тех случаях, когда все оборудование сгруппировано, чаще всего, в производственную линию с технологическим оборудованием, расположенным согласно ТП изготовления некой единицы планирования (ЕП), в качестве которой могут выступать отдельные детали или узлы.
Наличие горизонта планирования для всего множества заказов, присутствующих во множестве
говорит о том, что алгоритм системы планирования будет пытаться построить расписание в пределах этого горизонта. Отсутствие такого горизонта чаще всего характерно для систем планирования, в которых используется однопроходный эвристический алгоритм и в случае превышения горизонта планирования расписание не будет улучшаться. При выборе конкретных систем рекомендуется вариант с наличием горизонта планирования.
Признак «Вид критерия построения расписания» определяет – используется один некий критерий
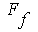или несколько, которые представлены вектором или функционалом
,
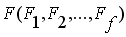состоящим из нескольких отдельных критериев. Во втором случае использование векторного критерия позволяет заложить в расписание сразу несколько требовании – минимизация состава и длительности операций по переналадке оборудования, равномерность загрузки оборудования и др.
Классификационные признаки систем планирования
Использование такого функционала накладывает дополнительные требования на алгоритм построения расписания, поскольку как допустимое, так и оптимальное решение, чаще всего, ищется в области компромиссов, – на области Парето [6].
Кроме того, количество отдельных критериев в таком функционале не может быть велико, так как их количество сказывается на эффективности получаемого решения, не говоря уже о том, что отдельные критерии, входящие в функционал, не должны быть противоречивы.
Характер критерия по отношению к портфелю заказов определяет, относится ли тот или иной критерий только к одной ЕП или некой группе из нескольких ЕП, либо этот критерий относится ко всей программе выпуска (портфелю заказов) и всему парку оборудования. Например, критерий минимума состава и длительности переналадок оборудования является общим как для всего парка оборудования, для которого ведется планирование, так и для всего портфеля заказов. Напротив, критерий минимума тех же затрат по переналадке по отношению к какой-либо конкретной i-й ЕП из портфеля заказов – это уже частный критерий. Частный критерий по отношению к портфелю заказов всегда выделяет ту или иную ЕП (или группу ЕП) относительно остальных ЕП во множестве M.
Характер критерия по достижению эффективности производственной системы определяет направленность критерия либо на конкретный показатель, либо на общий. Например, указанный ранее критерий минимума состава и длительности переналадок оборудования является частным, поскольку его выполнение гарантирует только минимизацию данных затрат. Затраты на транспортных и складских операциях, а также пролеживание ЕП при этом могут и возрасти. Надо сказать, что в этом плане большинство единичных критериев планирования относятся к частным по данному квалификационному признаку. Даже незыблемые вроде бы критерии типа минимума продолжительности выполнения всего плана работ также относятся к частным. Например, если во множестве M не две-три операции, а значительно больше, как это и бывает в реальных случаях (в мелкосерийном производстве участок из 100 ОУ за смену может «переварить» до 300 операций), оптимальному решению при использовании данного критерия всегда соответствует хотя бы одна последовательность операций a, b,…, c на некой ЕП, для которой суммарное время выполнения этой последовательности T нельзя уменьшить. Пример такой последовательности показан на рис.1. Хорошо, если мы сразу, на первых же итерациях поиска получили плотный по загрузке оборудования вариант «а», который высвободит нам сразу несколько ОУ. При этом высвободившихся рабочих мы можем переместить на другие участки, где есть потребность в рабочей силе. Если же получим вариант «б», характеризующийся, как мы видим, весьма неэффективным распределением операций между ОУ, то дальнейший поиск нам ничего не даст, т.к. величину длительности выполнения всего множества работ – T, мы не уменьшим. Алгоритм, руководствуясь таким критерием, честно просмотрев все варианты, даст нам график загрузки в виде «лоскутного одеяла», характеризующийся простоями оборудования, которые должны быть оплачены. Частный критерий в данном случае – это критерий, который отражает какую-либо одну особенность при построении расписания.
Рис.1. Особенности использования критерия минимизации
Количество критериев в системе планирования обычно бывает больше одного. Диспетчеру предлагается, исходя из конкретной производственной ситуации, выбрать тот или иной критерий планирования на расчетный период времени. Чем больше критериев в системе планирования, тем больше гибкость планирования и выше качество принимаемых решений. Системы с одним критерием встречаются достаточно редко и чаще всего относятся к классу APS. При этом единственный критерий планирования может отражать прибыль предприятия, полученную за единицу времени. В системах класса MES количество критериев планирования всегда должно быть больше одного.
Возможность расширения базы критериев как функция настройки системы пользователем, которому предоставляется возможность формирования определенных выражений с помощью базового алфавита и логических правил, встречается достаточно редко. Несмотря на то, что эта возможность резко повышает гибкость системы в плане настройки под конечного пользователя, имеются определенные сложности в реализации алгоритма построения расписания.
Вид алгоритма в системе планирования может быть декларирован какой угодно, но будет лучше, если эти декларации не будут носить маркетинговый характер, поскольку для нелинейных задач планирования, к которым относится подавляющее большинство аналогичных производственных задач, невозможно построить аналитический алгоритм, не свободный от известных проблем вычислительной сложности (NP-сложность). Практически все известные автору алгоритмы планирования для производственных систем всегда используют эвристический алгоритм. Тем не менее, ряд эвристических алгоритмов имеют очень неплохие показатели.
Характер алгоритма с точки зрения оптимизации говорит о том, что либо в системе при построении расписания используется процесс оптимизации, либо не используется. В первом случае не только появляется возможность нахождения улучшенного варианта расписания, то и повышается вероятность нахождения допустимого варианта за счет самой процедуры оптимизации. Второй случай является малопредпочтителеным. Проверить наличие функции оптимизации в алгоритме той или иной системы со стороны пользователя крайне сложно, поскольку алгоритм и программный код обычно защищены со стороны разработчика системы, хотя в практике имеются случаи, когда это можно было определить по косвенным показателям. Например, в работе [7] Д. Трич описывает ситуацию, когда покупатель предъявил и выиграл судебный иск против компании Э. Голдратта именно по вопросу об отсутствии заявленной оптимальности в системе планирования. Алгоритмы, получающие полностью оптимальное решение – крайне редкое явление, поскольку они в большинстве случаев используют, как уже было сказано выше, эвристические методы, которые, как правило, либо не обладают сходимостью, либо время сходимости столь велико, что о полной оптимизации можно забыть.
Регулирование глубины поиска в алгоритме – желательно, поскольку это позволяет в ряде случаев, не столь сильно ограниченных лимитом времени вычислений, получать лучшие решения относительно достигнутого допустимого.
Наличие множества решений алгоритма характерно для алгоритмов, имеющих процедуры оптимизации. Эта возможность, хотя и не так часто встречается ввиду сложности построения алгоритма, весьма полезна, поскольку позволяет получать диспетчеру ряд допустимых решений, из которых он может выбрать наиболее привлекательное по тем или иным конкретным причинам, не учтенным в аналитической форме.
Учитываемые классы ОУ – это признак, который говорит о том, какие классы ОУ могут быть учтены при построении расписания работы производственной системы. Традиционно в системах планирования учитывается только один класс ОУ – рабочие центры (РЦ) в виде множества технологического оборудования
.
Расписания для других классов ОУ – множества
транспортных средств
,
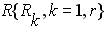складских систем
,
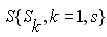бригад наладчиков
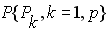
если и строятся, то, как правило, методом проекций [8] в виде расписаний, производных от расписаний основных ОУ – множества N. Это приводит не только к тому, что в дальнейшем они могут быть невыполнимы, но и к тому, что количество ОУ классов R, S, P получается сильно завышенным при крайне низкой загрузке. Например, при использовании существующих методов построения расписаний для вспомогательных ОУ их характер загрузки часто подчиняется Парето-распределению – степенная функция вида
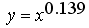, а при использование комплексной модели, которая учитывает в расписании все классы ОУ, – равномерному распределению (рис.2,а). Парето-распределение, которое получается в традиционных расписаниях, – весьма неблагоприятный вид распределения, который говорит о том, что 80% всей полезной работы приходится на 20% ОУ.
Рис.2. Последствия учета различных классов ОУ при различных подходах:
А – существующие подходы к учету ОУ; P – Парето-распределение; B – комплексные методы учета ОУ в расписаниях
До сих пор считалось, что Парето-распределение характеризует только социально-экономические процессы в обществе. Исследования, проведенные автором, показали, что принцип самоорганизации для технических систем, а метод проекций – это, по сути, и есть метод самоорганизации, является проигрышным вариантом. Использование комплексного подхода учета вспомогательных ОУ в моделях расписаний [8] показало, что: 1) сокращение количества вспомогательных ОУ достигает с 2-х до 10 раз; 2) повышение коэффициента загрузки вспомогательных ОУ достигает до 80%; 3) появляется возможность построения расписаний и возможность формирования управляющих программ для ОУ. Исходя из этого, крайне желательно, чтобы система планирования учитывала все интересующие производственников классы ОУ.
Характер технологических маршрутов по определению в теории расписаний может быть как фиксированным, так и не фиксированным. В первом случае ЕП проходят согласно ТП строго через определенные единицы технологического оборудования. Во втором случае появляется возможность пропустить те или иные ЕП через РЦ, которые являются альтернативными по методам обработки и достижимым параметрам точности и качества обработки. С точки зрения оптимальности получаемого расписания более предпочтительным является случай с нефиксированными маршрутами. При этом перед началом процесса планирования необходимо сформировать группы альтернативных РЦ.
Время переналадки оборудования в соответствии с характером технологических маршрутов может быть детерминированным или недетерминированным. В первом случае длительности всех операций ЕП считаются постоянными для любого РЦ из альтернативной группы оборудования (количество РЦ в альтернативной группе больше единицы). Во втором случае время переналадки зависит от того, на каком РЦ из альтернативной группы будет выполняться та или иная ЕП. Второй случай более предпочтительней, поскольку позволяет сэкономить, в среднем, 2-3% времени по отношению к усредненному варианту назначения указанных времен.
Учет последействия касается вопроса особенностей учета переналадки оборудования. Традиционный подход к определению величины состава и длительности операции переналадки РЦ заключается в том, что учитываются все требуемые операции из всего требуемого комплекса переналадок РЦ. При этом считается, что оборудование РЦ (станок, промышленный робот, накопитель деталей и пр.) в технологическом плане не соответствует вновь поступающей партии ЕП. Естественно, что в этом случае длительность комплекса переналадок
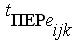принимается как максимальная с точки зрения длительности. При учете последействия вводится понятие состояния РЦ с точки зрения имеющихся на момент поступления на РЦ новой 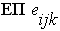технологических ресурсов [8].
Например, состав и длительность комплекса переналадок какой-либо k-й единицы РЦ с соответствующим составом ресурсов при поступлении партии ЕП зависит не только от требуемого состава технологических ресурсов для выполнения этой ЕП – , но также от состояния РЦ , которое сложилось на рассматриваемый момент назначения на всей предыстории планирования РЦ в течение смены (рис.3). При этом состав и длительность комплекса переналадок РЦ может изменяться от нуля (рис.3.а), – случай, когда все требуемые ресурсы , необходимые для выполнения ЕП имеются в составе РЦ, до максимального значения (рис.3.в), – в этом случае множество не включает в себя множество . Данный метод учета переналадок позволяет существенно повысить точность составления расписания и загрузку РЦ.
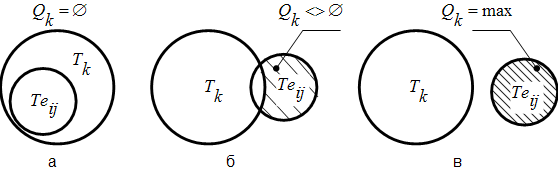
Рис.3. Учет последействия при оценке переналадок
Планирование на множестве альтернативных ТП, которое существенно повышает гибкость планирования и загрузку оборудования, возможно только в том случае, если имеющаяся САПР ТП поддерживает возможность формирования множества альтернативных ТП (АТП) по отношению к базовому варианту. Разработка АТП в традиционном варианте – процесс весьма трудоемкий, но если САПР ТП имеет возможность представления ЕП не только в виде операций, но также в виде технологических переходов, то на основе базового варианта ТП при использовании инструмента размерного анализа [9] появляется возможность создания множества АТП по точности не уступающих базовому варианту ТП [10].
Параметры обслуживания транспортно-накопительной системы и др. элементов могут быть как усредненными, так и расчетными (аналитическими). Первый случай, который является общепринятым, является допустимым, но во втором случае, когда, например, время транспортирования для транспортного средства определяется с учетом вычисленного кратчайшего маршрута, или аналитически определяются длительности всех вспомогательных операций [8], повышается точность составления расписания.
Прерывание партий запуска является классической характеристикой расписаний [3, 4]. Возможность прерывания появляется только для непрерывных процессов без последействия, например, для вычислительных систем. В машиностроении, которое характеризуется дискретным характером производства, прерывания партий запусков нежелательны как с точки зрения невозможности прерывания большинства операций по технологическим причинам, так и по причине возрастания количества и общей длительности процессов переналадки оборудования.
Целостность передачи партий запуска отражает возможность передачи уже обработанных отдельных ЕП (деталей, узлов) на другую операцию, не дожидаясь окончания выполнения всей партии ЕП. Если такая возможность имеется (отсутствует требование по целостности партии запуска при передаче), то это значительно повышает гибкость планирования и плотность загрузки оборудования (рис.4), однако реализация этой возможности имеет определенные сложности в плане построения алгоритма планирования, поэтому не все системы планирования имеют такую возможность.
Поддержка нерегулярности партий запуска ЕП означает возможность формирования на одном РЦ некой партии из разнородных партий ЕП с общностью по получаемым на технологической операции поверхностям обработки, например, обработка одинаковых по размерам и качеству поверхностей на различных деталях. Такие партии запуска непостоянны и могут образовываться каждый раз для различных деталей на различных операциях, т.е. в данном случае мы имеем дело с запуском в производство укрупненных партий в виде нерегулярных единиц планирования (НЕП), поскольку данные партии, представляющие нерегулярные множества [11]
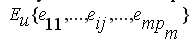при поступлении на какой-либо k-й РЦ могут образовываться различными как по наименованию ЕП , входящих в НЕП, так и по номеру операции (рис.5). При этом на каком-либо k-м оборудовании будут обработаны детали различных наименований, и данная операция для каждого наименования может быть любой по порядку следования в ТП данной детали [8]. После обработки НЕП каждая ЕП может продолжать свой процесс движения по цеху согласно своему ТП, либо вновь объединяться в НЕП.
Рис.4. Целостность передачи партии запуска
Рис.5. Нерегулярные партии запуска
Нерегулярные партии запуска часто формируются на операциях, которые принято называть технологическими сборами, когда на одной операции, с целью повышения точности сопряжения, обрабатываются две или более деталей, входящих в сборочную единицу. Возможность оперирования нерегулярными партиями запуска в системе планирования – желательна.
Характер единиц планирования указывает на то, чем может оперировать та или иная система планирования – только отдельными деталями или сборочными единицами (комплектами, узлами, готовыми изделиями). Крайне желательным является вариант учета сборочных единиц, поскольку он является наиболее общим случаем. При этом директивные сроки выполнения заказов
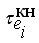указываются не на отдельные детали, а на сборочную единицу верхнего уровня. Моменты окончания обработки и сборки отдельных деталей и узлов должны определяться в процессе построения расписания исходя из ненарушения сроков .
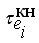Учет емкости склада в системах планирования подразумевает, что планирование всей программы ведется с учетом предельной емкости склада готовой продукции или промежуточного склада. При этом расписание строится исходя из того ограничения, что емкость склада не может быть превышена. Используется в случае, когда склад является лимитирующим фактором. При этом склад в математических моделях является ОУ с соответствующими параметрами: длительностью обслуживания, количеством операторов и пр.
Учет незавершенного производства в подавляющем большинстве случаев должен присутствовать в системе планирования, поскольку этот фактор определяет не только величину связанного капитала, но и общую эффективность производственной системы.
Возможность построения межцеховых расписаний в большей степени присуща APS-системам, но может присутствовать и в MES-системах [8]. Существующие методы построения межцеховых расписаний на основе межцеховой кооперации характеризуются существенными потерями времени ввиду укрупненной оценки времени выполнения заказа тем или иным цехом. Предпочтительным в системах планирования является вариант построения межцеховых расписаний, который оперирует комплексной математической моделью, отражающей критерии и ограничения всех цехов. Такая возможность легко реализуется в APS-системах, поскольку в них чаще всего ведется планирование для всего предприятия по одному критерию – максимизации прибыли за единицу времени. Если межцеховое расписание строится только для определенной группы цехов, то в модели планирования необходимо учитывать ограничения и критерии этих цехов, т.е. переходить к комплексному характеру построения модели планирования [12].
Однородность моделей планирования для случая межцеховых расписаний облегчает построение как моделей, так и расписаний в последствии, но эта однородность наблюдается далеко не всегда, поскольку каждый цех может характеризоваться, в силу конкретных производственных ситуаций, собственными критериями и ограничениями в модели. Желательно, если система планирования в состоянии учитывать неоднородность моделей.
Наличие системы расчета или назначения приоритетов для ЕП означает возможность планирования с учетом приоритетов для тех или иных ЕП. Как мы уже сказали выше, приоритеты типа FIFO и др., взятые из теории массового обслуживания, мало что дают в реальности, поскольку каждая ЕП не только может характеризоваться собственными сроками сдачи, но и трудоемкостью. Поэтому расчет приоритетов должен быть чем-то обоснован, базироваться на анализе проблемы. Например, приоритет ЕП, назначенный на основе напряженности заказов [8] позволяет быстрее выпустить те ЕП, которые имеют минимальный резерв времени. В то же время данная характеристика больше относится к алгоритмической части системы, к анализу номенклатуры запуска перед процедурой планирования.
Учет многостаночности характеризует возможность системы планирования загружать на какие-либо ОУ в один и тот же интервал времени различные работы. Эта характеристика отражает не только реальные случаи многостаночного обслуживания в цеху, но и возможность планирования бизнес-процессов (рис.6), когда за одним и тем же исполнителем закрепляется несколько различных работ.
Рис.6. Учет многостаночности
Наличие функции диспетчирования означает возможность контроля хода выполнения исполняемого плана относительно расчетных данных. При этом в режиме времени с дискретой, равной минимальной длительности любого действия (технологическая операция, переналадка оборудования и т.п.), производится анализ запаздывания или опережения всех работ на всех ОУ.
Возможность пересчета расписания появляется только при наличии функции диспетчирования. При этом при пересчете должны учитываться: текущие данные по незавершенному производству, сроки выпуска продукции, возможность использования иных критериев построения расписания работ.
В рассмотренной классификации не приводятся характеристики, которые являются не столь важными с точки зрения качества получаемых решений и более относящихся к технической реализации, например, сетевой или локальный вариант системы планирования, возможность интеграции с системами САПР ТП, PDM/PLM, протоколы передачи данных и пр.
Автор не стал придавать формальный вид характеристикам, как это принято в теории расписаний [3, 4], поскольку при большом количестве характеристик формализация записи теряет смысл краткой нотации. Кроме того, классификация может не исчерпываться указанным составом классификационных признаков, поскольку те или иные особенности конкретного производства могут вносить свои дополнения. Главное при этом, чтобы новые классификационные признаки отражали особенности планирования и качество принимаемого решения.
Таким образом, при выборе системы планирования любого уровня – ERP, APS, MES, необходимо, прежде всего, обратить внимание на важность для конкретного производства тех или иных классификационных признаков и наличие соответствующих функций в выбираемой системе.
При желании на базе рассмотренных классификационных признаков можно решить задачу оптимизации на векторном критерии с целью выбора оптимальной для предприятия системы планирования.
©Загидуллин Р.Р. докт. техн. наук, профессор каф. АТП Уфимского Государственного Авиационного Технического Университета
©12NEWS
Литература
1. Загидуллин Р. Р., Фролов Е. Б. Управление машиностроительным производством с помощью MES-систем. М.: СТИН, 2007, №11, С.2–5.
2. Загидуллин Р. Р., Драган В. Ф., Степанов В. Е., Камалетдинов Т. Р. Интеграция систем конструкторско-технологической подготовки и управления производством в структуре АСУП. М.: СТИН, 2007, №10, С. 2 – 5.
3. Танаев В. С., Гордон В. С., Шафранский Я. М. Теория расписаний. Одностадийные системы. – М.: Наука, – 1984. – 384 с.
4. Танаев В. С., Сотсков Ю. Н, Струсевич В. А. Теория расписаний. Многостадийные системы. – М.: Наука, – 1989. – 328 с.
5. Смоляр Л.И. Модели оперативного планирования в дискретном производстве. – М.: Наука, – 1978, – 320 с.
6. Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. М.: ФИЗМАТЛИТ. – 2002. – 144 с.
7. Д. Трич. Почему метод критического пути под любым другим названием не становится лучше? К созданию целостного подхода к PERT/CRM. Управление проектами и программами. – № 1(05) 2006. – С.4 – 22.
8. Загидуллин Р.Р. Оперативно-календарное планирование в гибких производственных системах. М.: Изд-во МАИ, 2004. – 208 с.
9. Балакшин Б.С. Основы технологии машиностроения. М.: Машиностроение, – 1969. – 358 с.
10. Загидуллин Р.Р. Проектирование и планирование технологических процессов в ГПС на базе дифференциации операций. СТИН, – 2002, – № 6., с. 15 – 19.
11. Рейуорд - Смит В.Дж. Теория формальных языков. Вводный курс: Пер. с англ. – М.: Радио и связь, –1988, – 128 с.
12. Загидуллин Р.Р. Построение моделей межцеховых расписаний в подсистемах оперативно-календарного планирования автоматизированных производств. – СТИН, №8, 2004, С.3 – 8.
© Галактика, 2010
© Издание 12NEWS (ИП Маринин А.Л.), 2010
